Derivative Of Log Base 2 Of X
Click on SOLVE to process the function you entered. Thus ln x2 2 ln x.
What Is The Derivative Of Log 2x Quora
Binary logarithm of value a is the power x raised to number 2.

Derivative of log base 2 of x. Where b 0 and not equal to 1 then the derivative is equal to the original exponential function multiplied by the natural log of the base. Dfracddx adisplaystyle x adisplaystyle xlog_ea The derivative of an exponential function is equal to the product of the exponential function and natural logarithm of the base of exponential function. And now we can use the chain rule to evaluate this derivative.
Topic 20 of Precalculus. The logarithm of x to a power n equals n times the logarithm of x. Derivative of the Exponential Function.
So to find the second derivative of sin2x we just need to differentiate 3sin 2 xcosx. We can use the product rule and trig identities to find the derivative of 3sin 2 xcosx. Derivative of an exponential function in the form of.
F x 1 x lnb x is the function argument. Log 3 50 log 8 50 log 8 3 18812853 05283208 35608766. Derivative of Log e.
The last thing that we want to do is to use the product rule and chain rule multiple times. Since you have a constant raised to the variable x the. 2 x n.
The formula for. For any real number x log base 2 functions are written as. Note that the logarithm of base 0 does not exist and logarithms of negative values are not defined in the real number system.
Y lnx y0 1 x0 1 ey 1 x. Note that the derivative x0of x ey is x0 ey x and consider the reciprocal. Derivative of given polynomial is.
Y log 2 6x log 2 6 log 2 x. From above we found that the first derivative of sec2x 2sec 2 xtanx. 9x2 8x1 6 Now put x 2 94 82 6 36 16 6 58 Input.
This is an example of a simple logarithm as it basically counts the number of multiplications of the same factor - in this case 2. For example log 2 32 5 since 2 5 32. The expression for the derivative is the same as the expression that we started with.
3x3 4x2 6x1 89x0 2 Output 58 Explanation. Leaving us with the derivative of ln x which is 1x The constant 2 comes out of the differentiation. Ln e x ln 62.
Log base 2 is the power to which the number 2 must be raised to obtain the value of n. It is called the derivative rule. Calculate the limit of that derivative.
If we need a decimal value we can work it out using change of base as follows. Parentheses are sometimes added for clarity giving lnx log e x or logx. Find the derivative of.
Here are a few examples of what you can enter. So to find the second derivative of sec2x we need to differentiate 2sec 2 xtanx. Log a n x.
The natural logarithm of a number is its logarithm to the base of the mathematical constant e which is an irrational and transcendental number approximately equal to 2718 281 828 459The natural logarithm of x is generally written as ln x log e x or sometimes if the base e is implicit simply log x. The natural log function and its derivative is defined on the domain x 0. So we have d dx log a x 1 x 1 lna 1 xlna.
To calculate the second derivative of a function differentiate the first derivative. Ln b is the natural logarithm of b. According to the rule for changing from base e to a different base a.
Solve e x 62. F x log 2 x f. The derivative of the second term is as follows using our formula.
The second derivative of lnx is -1x 2This can be derived with the power rule because 1x can be rewritten as x-1 allowing you to use the rule. The derivative of lnk where k is any constant is zero. The 2 multiplied by 1x is written as 2x.
B is the logarithm base. Definition with hyperreals Relative to a hyperreal extension R R of the real numbers the derivative of a real function y f x at a real point x can be defined as the shadow of the quotient y. The derivative of logarithmic function of any base can be obtained converting log a to ln as y log a x lnx lna lnx 1 lna and using the formula for derivative of lnx.
The log to the base 2 is called as binary logarithm. Dydxlog_2e 1xlog_2ex The term on the top log 2 e is a constant. The first term log 2 6 is a constant so its derivative is 0.
Please try your approach on IDE first before moving on to the solution. From above we found that the first derivative of sin3x 3sin 2 xcosx. In previous lessons or courses youve learned about ways to define E and this could be a new one.
The notation is log b x or log b x where b is the base and x is the number for which the logarithm is to be found. Log 2 100 log 10 100 log 10 2 2 030103 664386. Find the derivative of.
Use x as your variable. B when x is less than 1 and becomes smaller. So what we will do is we will first take the derivative of the outside function.
The functions fx sinxx and gx cosxx are two of the simplest examples of non-integrable functions meaning their antiderivatives cannot be expressed in terms of elementary functionsNo matter how you attempt u-substitution or integration by parts on sinxx or cosxx you will always end up with another non-integrable function. This logarithm is generally used in bioinformatics. E is the number that where if you take that number to the power of X if you define a function or expression as E to the X its that number where if you take.
The Second Derivative Of sin3x To calculate the second derivative of a function you just differentiate the first derivative. Derivative of Logarithm. Use the keypad given to enter functions.
So e to the natural log of a times x with respect to the inside function with respect to natural log of a times x. That is e x. X log 2 n.
We can use the product and chain rules and then simplify to find the derivative of 2sec 2 xtanx. A when x is greater than 1 and becomes larger. And so this is going to be equal to e to the natural log of a times x.
1x3 3 Output. The derivative of e x is quite remarkable. Since the natural log function to the base e log e e is equal to 1 The derivative of log e is equal to zero because the derivative of any constant value is equal to zero.
Log b x log c x log c b Example 1. The known derivatives of the elementary functions x 2 x 4 sinx lnx and expx e x as well as the constant 7 were also used. The base b logarithm of x is equal to the base c logarithm of x divided by the base c logarithm of b.
When the logarithmic function is given by. A word formed by derivation. The Second Derivative Of sec2x.
Sample Problem Question. Raising b with the power of base b. Find the base 2 logarithm of value using this calculator.
F x log b x The derivative of the logarithmic function is given by. Taking the natural log on both sides it becomes. Fx ln1 x1 x 2 2 1 x 3 3.
That derivative becomes. E x 62. Which is equal to.
That derivative approaches 0 that is becomes smaller. The derivative of log a x. Ie log 2 a x where 2 x a.
Noun a word formed from another word or base.
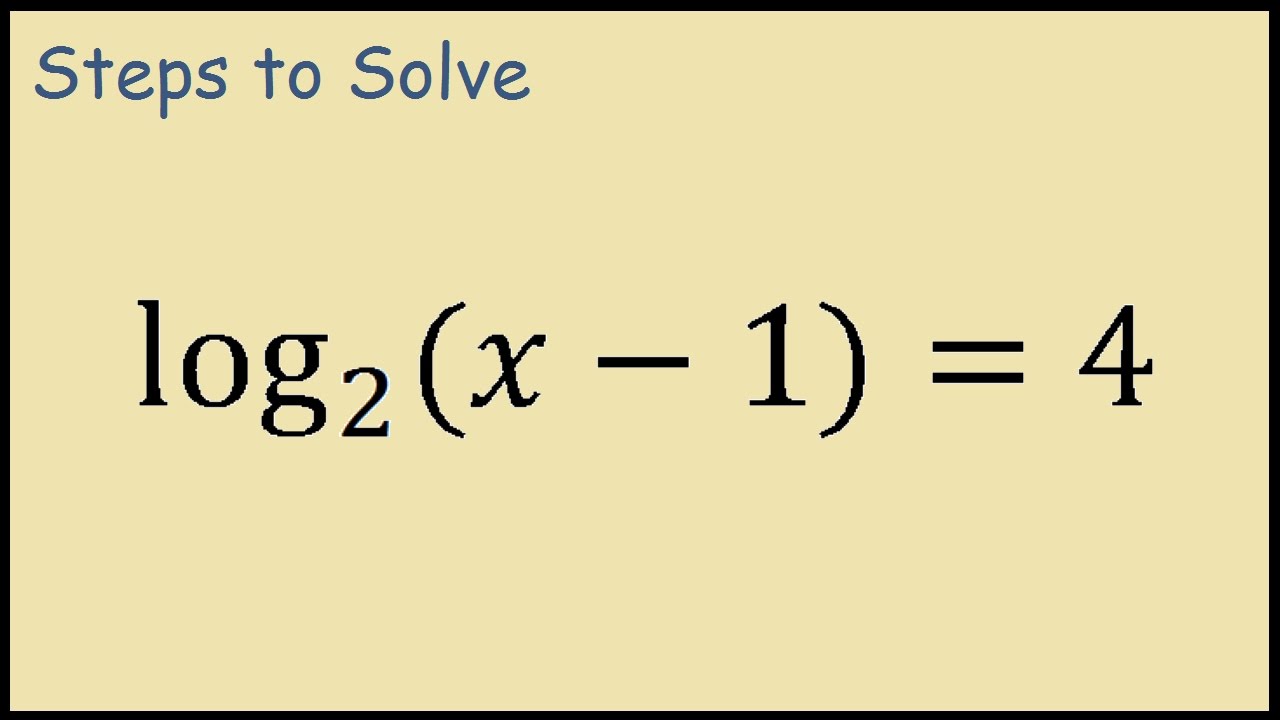
Log2 X 1 4 Solving Logarithm Problem By Hand Youtube
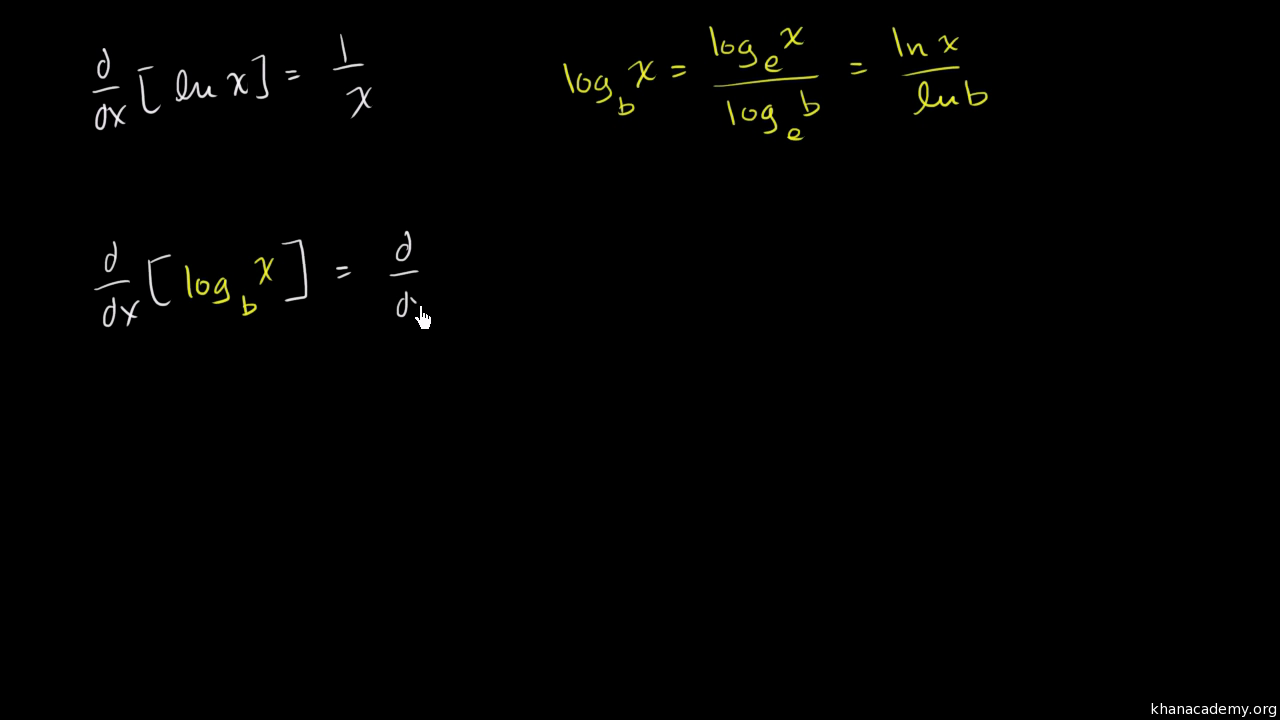
Derivative Of Logarithm For Any Base Old Video Khan Academy
Differentiating Logarithmic Functions Review Article Khan Academy
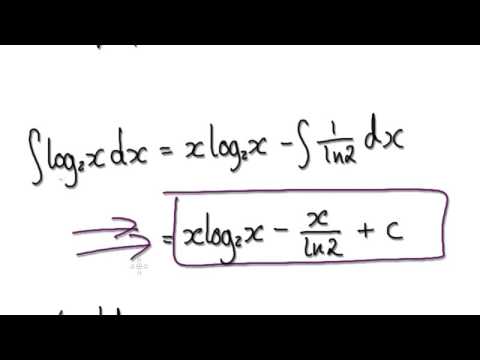
Video 1959 Differentiate Log Base 2 And Integrate Log Base 2 Practice Youtube
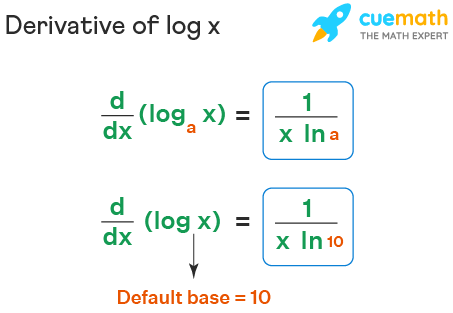
Derivative Of Log X Formula Proof Examples

Finding The Derivative Of Log X Video Lesson Transcript Study Com

Finding The Derivative Of Log X Video Lesson Transcript Study Com

Ex 1 Derivative Of The Log Function Not Base E Youtube

Video 1959 Differentiate Log Base 2 And Integrate Log Base 2 Practice Youtube
What Is The Differentiation Of Log Base X Of A Quora
Derivative Of Logarithm For Any Base Old Video Khan Academy

Find Second Derivative Of Log X Calculus Youtube

Logarithmic Differentiation W 7 Step By Step Examples

Log2 1 16 X How To Solve Logs By Hand Youtube
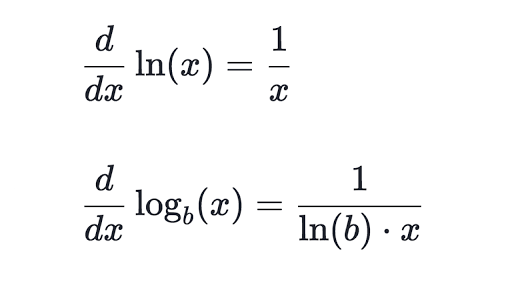
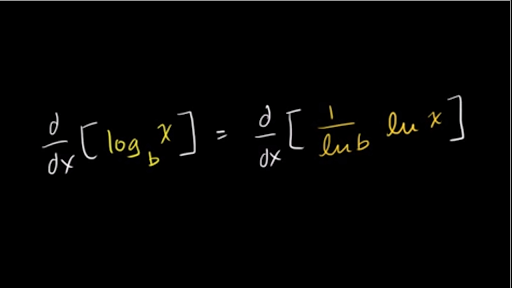
Posting Komentar untuk "Derivative Of Log Base 2 Of X"