Why Sqrt 2 Is Irrational
So the square root of 2 is irrational. P q have no common factors other than 1.

How To Adapt Proof By Contradiction Showing That A Sqrt 2 Is Irrational For Sqrt 20 Mathematics Stack Exchange
Ab b0 Where a and b are integers.

Why sqrt 2 is irrational. Tell why it fits that category. This indirect proof shows why the sum of a rational and an irrational number will always be an irrational number. And so the square root of 2 cannot be written as a fraction.
So the square root of 2 is irrational. Join the TEDSF QA learning community and get study support for success - TEDSF QA provides answers to subject-specific questions for improved outcomes. 2 a2 b2 And lets multiply both sides by b 2 2b2 a2.
We call such numbers irrational not because they are crazy but because they cannot be written as a ratio or fraction. By the Pythagorean Theorem the length of the diagonal equals the square root of 2. Some square roots like 2 or 20 are irrational since they cannot be simplified to a whole number like 25 can be.
We want to show that A is true so we assume its. The proof goes like this. Prove that sqrt2 rational 2 non integer.
College Algebra playlist but its important for all mathematicians to learnTori proves using contradiction that th. When evaluated produces a number that has a non terminating and non repeating decimal part. Why is square root of 2 an irrational number.
Numbers that are rational can all be written in the form. According to our assumption sqrt 2 is rational and therefore can be represented as a ratio of two integers a and b where the ratio of ab is irreducible and where a and b share no common factors other than 1 sqrt 2 ab a b integers ab irreducible Now lets square both sides. Odd number times odd number is always odd.
Product of two irrational numbers can be both rational for example sqrt 2 cdot sqrt 05 sqrt 1 1 or irrational your example so the fact that sqrt 2 and sqrt 3 are irrational is not a proof that sqrt 6 is irrational. Specifically the Greeks discovered that the diagonal of a square whose sides are 1 unit long has a diagonal whose length cannot be rational. From the equality 2 ab it follows that 2 a 2 b 2 or a 2 2 b 2.
Non terminating decimal number that have repeating digits can be written in this form so are called rational numbers. Because it cant be odd. But there are lots more.
The proof of the irrationality of root 2 is often attributed to Hippasus of Metapontum a member of the Pythagorean cult. They go on forever without ever repeating which means we cant write it as a decimal without rounding and that we cant write it as a fraction for the same reason. Sqrt22sqrt12 2sqrt12 as sqrt2 is an irrational no its reciprocal is also an irrational no.
Specifically the Greeks discovered that the diagonal of a square whose sides are 1 unit long has a diagonal whose length cannot be rational. So the square root of 2 is irrational. By the Pythagorean Theorem the length of the diagonal equals the square root of 2.
From this we know that a itself is also an even number. Lets imagine that there is a rational number p q 2. Find the sum of eq5 sqrt2 eq.
Why Is The Square Root Of 2 An Irrational Number. Assume the negation of the original statement is true. If b is odd then b 2 is odd.
Specifically the Greeks discovered that the diagonal of a square whose sides are 1 unit long has a diagonal whose length cannot be rational. Where p q is a fraction in its simplest form - ie. Simple Sqrt2 is an irrational Number.
By the Pythagorean Theorem the length of the diagonal equals the square root of 2. Similarly if b is even then b 2 a 2 and a are even. Therefore 2 non integer.
Is sqrt2 an example of a rational terminating rational repeating or irrational number. This proof technique is simple yet elegant and powerful. The square root of 2 is irrational It is thought to be the first irrational number ever discovered.
3b 2 a 2. Specifically the Greeks discovered that the diagonal of a square whose sides are 1 unit long has a diagonal whose length cannot be rational. Since any choice of even values of a and b leads to a ratio ab that can be reduced by canceling a common factor of 2 we must assume that a and b are odd and that the ratio ab is.
P q which is the square root of two. In this case a 2 and a are also odd. This video is housed in our WCoM Basics.
Basic steps involved in the proof by contradiction. Check it if you dont believe me. Why is the square root of 2 irrational.
It is irrational because it is impossible to write a rational number ie. Join the TEDSF QA community and get support for success - TEDSF Q. He is said to have been murdered for his discovery though historical evidence is rather murky as the Pythagoreans didnt like the idea of irrational numbers.
By the Pythagorean Theorem the length of the diagonal equals the square root of 2. The following proof is a classic example of a proof by contradiction. By the Pythagorean theorem an isosceles right triangle of edge-length 1 has hypotenuse of length sqrt2 If sqrt2 is rational some positive integer multiple of this triangle must have three sides with integer lengths and hence there.
This note presents a remarkably simple proof of the irrationality of sqrt2 that is a variation of the classical Greek geometric proof. Proving that color redsqrt 2 is irrational is a popular example used in many textbooks to highlight the concept of proof by contradiction also known as indirect proof. If sqrt2 rational let a and b be integer such as gcdab1 and sqrt2ab.
Since sqrt2 rational 2 non integer and knwoing that 2. If a itself was odd then a a would be odd too. 3 a 2 b 2.
So the square root of 2 is irrational. So the square of a is an even number since it is two times something. MathsHeres one of the most elegant proofs in the history of maths.
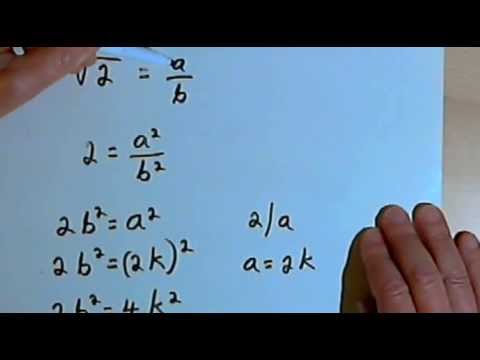
Proof That The Square Root Of 2 Is Irrational 127 4 21 Youtube
The Square Root Of Two Making Your Own Sense

Lc Hl Prove That Root 2 Is Irrational Youtube
The Square Root Of Two Making Your Own Sense

How To Adapt Proof By Contradiction Showing That A Sqrt 2 Is Irrational For Sqrt 20 Mathematics Stack Exchange
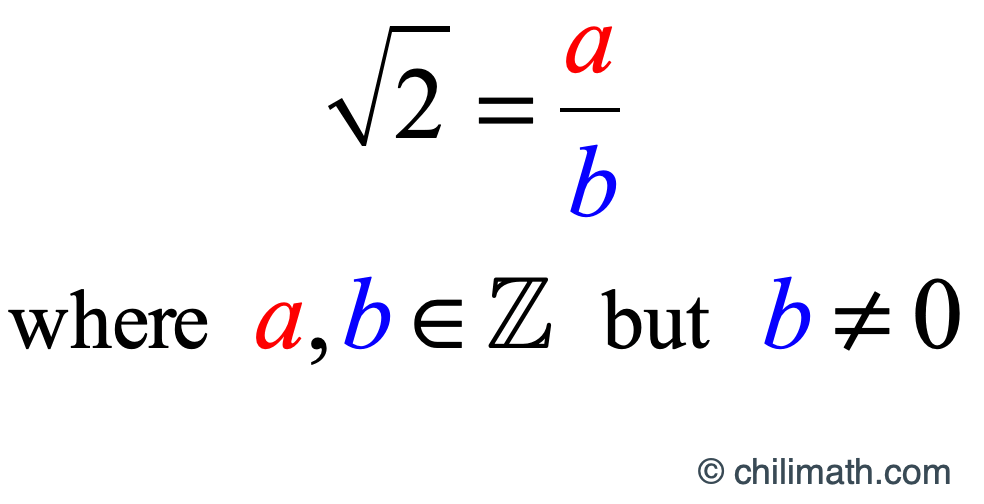
Proof 2 Is Irrational Chilimath

Prove That Root 2 Is Irrational Number Is Root 2 An Irrational

Prove Root 2 Is Irrational Prove Root 2 Is Irrational That Flickr

Theorem 1 4 Root 2 Is Irrational Chapter 1 Real Number Class 10th In Hindi Youtube

Irrationality Of The Square Root Of 2

Understanding The Proof Of Sqrt 2 Is Irrational By Contradiction Mathematics Stack Exchange

Prove That Square Root Of 2 Is Irrational Using The Principle Of Mathematical Induction Mathematics Stack Exchange
The Square Root Of Two Making Your Own Sense

Prove 1 Root 2 Is Irrational No Mathematics Topperlearning Com Qx47s8dd
Posting Komentar untuk "Why Sqrt 2 Is Irrational"