When Does A Function Have An Inverse

Oleh cilung Oktober 10, 2022 Posting Komentar

A function has an inverse if and only if it is a one-to-one function. Function pairs that exhibit this behavior are called inverse functions.

Inverse Functions

To use an example f x f x is one-to-one if and only if for every value of f x there is exactly one value of x that gives that value.

When does a function have an inverse. A function has an inverse if and only if it is a one-to-one function. Is the inverse of a function always a function. The inverse of a function may not always be a function.

A function f x has an inverse function if f x is one-to-one. F xx² does not have an inverse function. Experts are tested by Chegg as specialists in their subject area.

A function is said to be one-to-one if for each number y in the range of f there is exactly one number x. Theres an easy way to look at it then theres a more technical way. Inverse functions are a way to undo a function.

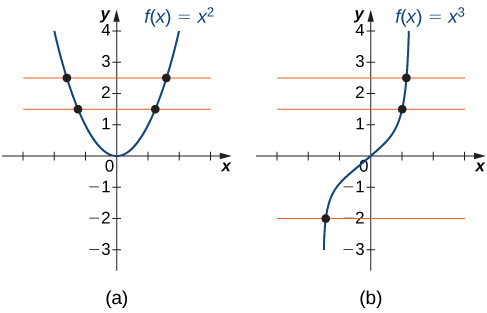
Y x2 where the domain is the set of real numbers does not have an inverse because the square root function is a one-two-two mapping except at 0. You know Im going to tell you what one-to-one is. It is a relation that swaps the roles of the two sets.

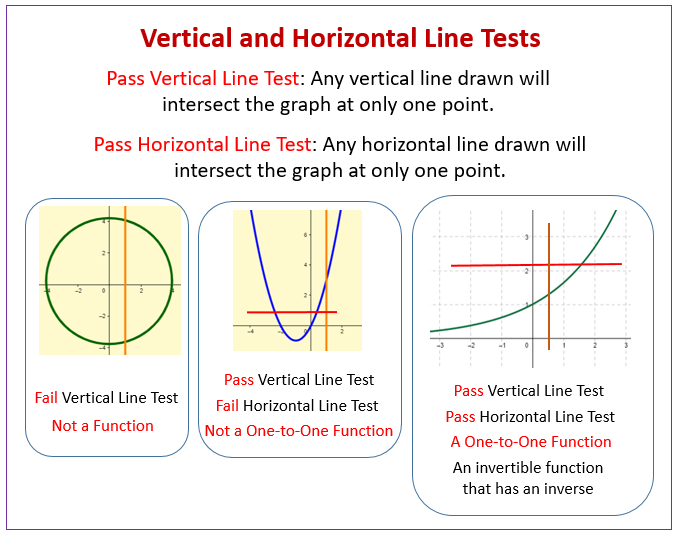
To use an example f x f x is one-to-one if and only if for every value of f x there is exactly one value of x that gives that value. An inverse function essentially undoes the effects of the original function. A graph represents a one-to-one function if and only if it passes both the vertical and the horizontal line tests.

If no horizontal line intersects the graph of f more than once then f does have an inverse. For a function its inverse admits an explicit description. Y X If f isnt surjective then there are elements of Y that dont have anything in X mapped to them.

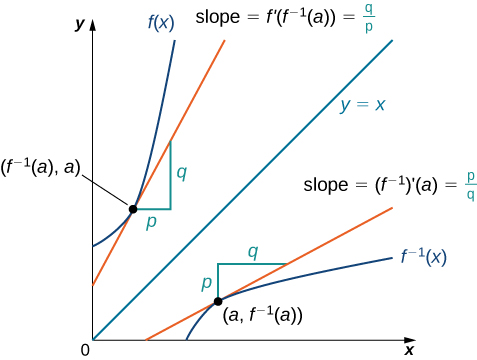
Before formally defining inverse functions and the notation that were going to use for them we need to get a definition out of the way. Since 2009 the ISO 80000-2 standard has specified solely the arc prefix for the inverse functions. In the original function plugging in x gives back y but in the inverse function plugging in y as the input gives back x as the output.

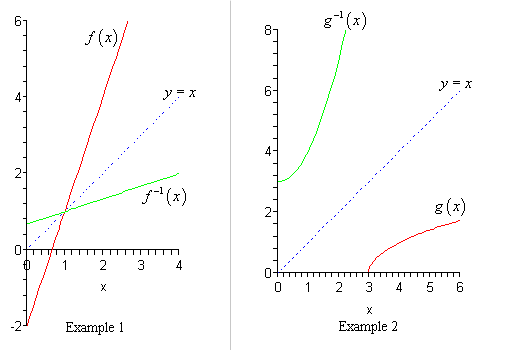
In mathematics the inverse function of a function f also called the inverse of f is a function that undoes the operation of f. Any polynomial with more than one root over. If you want to think about this graphically f x and its inverse function will be reflections across the line y x.

A function is called one. If a function were to contain the point 35 its inverse would contain the point 53If the original function is fx then its inverse f -1 x is not the same as. A function f x has an inverse or is one-to-one if and only if the graph y f x passes the horizontal line test.

Example of a graph with an inverse Example of a graph without an inverse The following are the main strategies to algebraically solve for the inverse function. Given a function f x it has an inverse denoted by the symbol color red f - 1left x right if no horizontal line intersects its graph more than one time. The property of having an inverse is very important in mathematics and it has a name.

Click to see full answer. If any horizontal line intersects the graph of f more than once then f does not have an inverse. If f x says to multiply by 2 and then add 1 then the inverse f x will say to subtract 1 and then divide by 2.

It is possible that only one of these formulas hold. Thats very helpful Come on. Thanks a heap math geek lady.

Inversef xln x-5 inversef xfrac 1 x2 inverseyfrac x x2-6x8 inversef xsqrt x3 inversef xcos 2x5 inversef xsin 3x pre-calculus-function-inverse-calculator. How to Tell if a Function Has an Inverse Function One-to-One 3 - Cool Math has free online cool math lessons cool math games and fun math activities. Have I let you down yet.

Since none of the six trigonometric functions are one-to-one they must be restricted in order to have inverse functions. An inverse of a function is one that has as its domain the original codomain and as its codomain the original domain. It sends each element to the unique element such that fx y.

That is for every element of the range there is exactly one corresponding element in the domain. Basic concepts Principal values. How do you know if a function is constant.

Also to know is why would a function not have an inverse. The inverse of f exists if and only if f is bijective and if it exists is denoted by. That is for every element of the range there is exactly one corresponding element in the domain.

I know what youre thinking. If we try to. Some functions do not have inverse functions.

Really clear math lessons pre-algebra algebra precalculus cool math games online graphing calculators geometry art fractals polyhedra parents and teachers areas too. An important property of the inverse function is that inverse of the inverse function is the function itself. Inverseyfrac x2x1 x inversef xx3.

Inverse function for a function yfx is such function xgy that gfxx for all values of x where f is defined. We review their content and use your feedback to keep the quality high. View the full answer.

Functions that have inverse are called one-to-one functions. A function y f x has an inverse if there exists another function y g x such that for all x f g x x and g f x x. So how do we prove that a given function has an inverse.

In that case we would talk about right and left inverses.

Inverse Functions